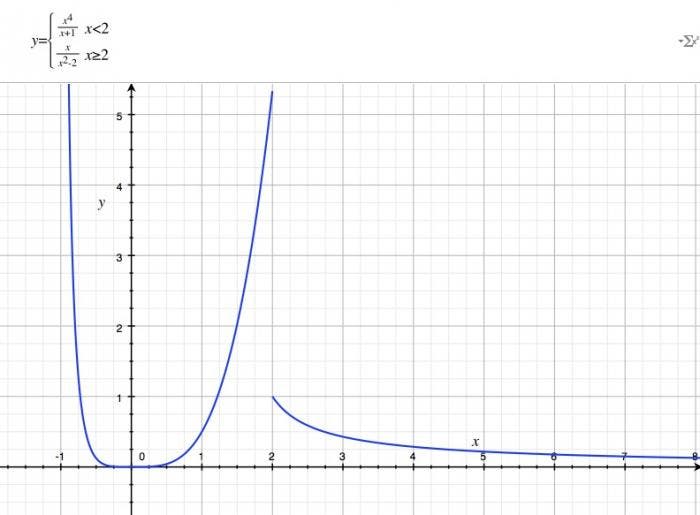
A primero de ingeniería de la mayoría de carreras técnicas se enseña en análisis y álgebra las funciones a trozos. Más bien se enseñan en bachillerato y se trabajan en la universidad donde se le dan más sentido. Con Grapher también se pueden representar para entender mejor con qué estamos trabajando. En genial estar en clase y poder ver lo que te explica el profesor sin tener que imaginártelo sin más.
Para empezar con la función a trozos debemos abrir la llave de condiciones, la encontraremos en la paleta de ecuaciones. Al hacer clic Grapher nos va a pedir cuantas condiciones le queremos en la función: 1, 2, 3…
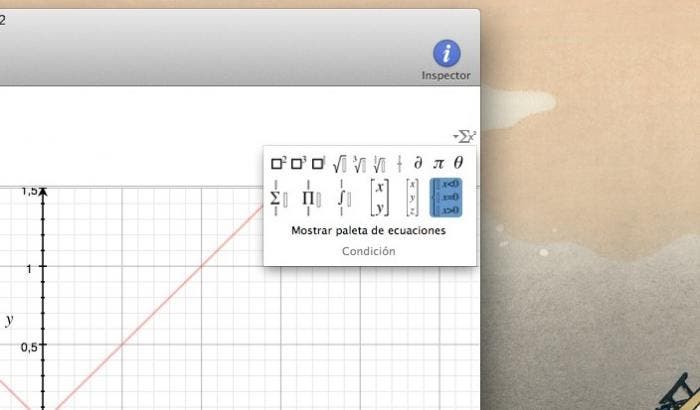
Lógicamente en primer lugar debemos especificar la función y por el otro lado la condición en sí. Hasta aquí nadie que conozca mínimamente las funciones a trozos y el lenguaje matemático–informático tendría que tener problemas, pero como hemos visto en capítulos anteriores, Grapher es especial. ¿Qué pasa si necesitamos expresar una condición tal y como 1 > x > 3? El truco está en definir las desigualdades por separado y con un ampersand & o dos puntos :.
Si seguimos con un ejemplo de función definida a trozos, podemos representar la siguiente función.
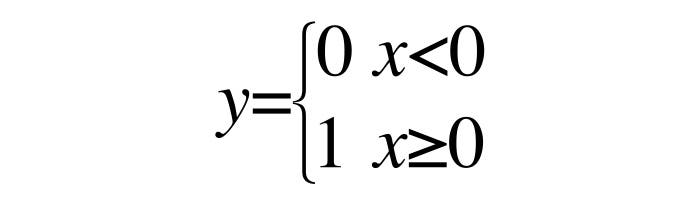
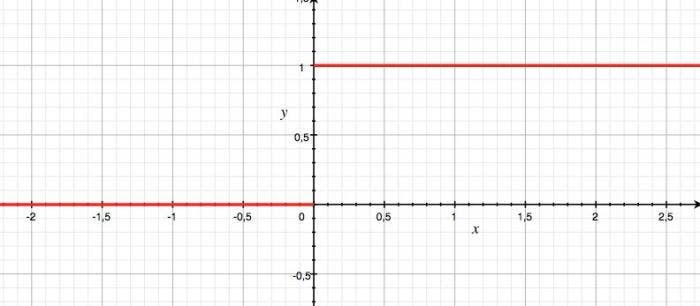
Esta función es la función escalón de Heaviside o del escalón unitario. Es tan sencilla como que para valores negativos la función es 0 y para valores positivos la función es 1. Se utiliza para el procesamiento de señales o en ingeniería de control
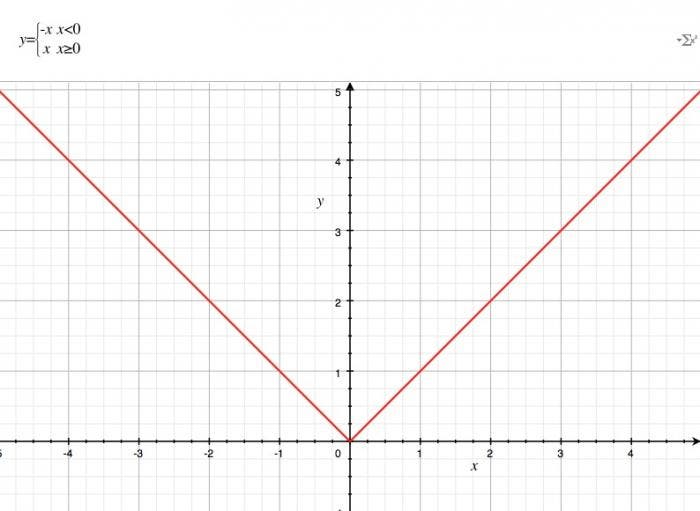
La función del valor absoluto es una de las primeras que se enseña y es la más fácil de entender.
Pues ahora ya podemos trabajar continuidad con funciones definidas a trozos. Este ha sido un capítulo muy corto pero necesario para poder trabajar con funciones a trozos. En este tipo de funciones también pueden usarse como condiciones otros operadores como si…entonces o si…entonces…si no como ? o : y ?: o ::* respectivamente.